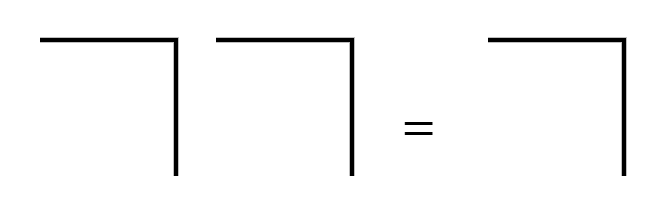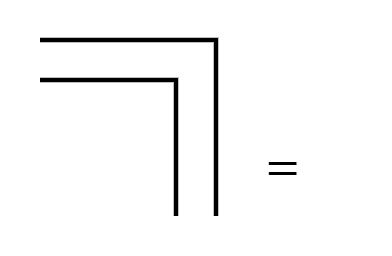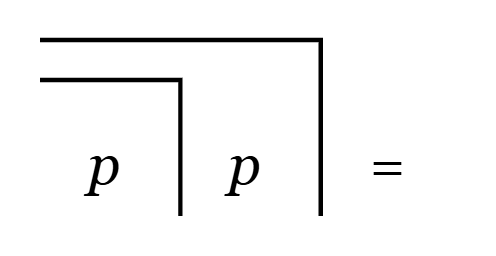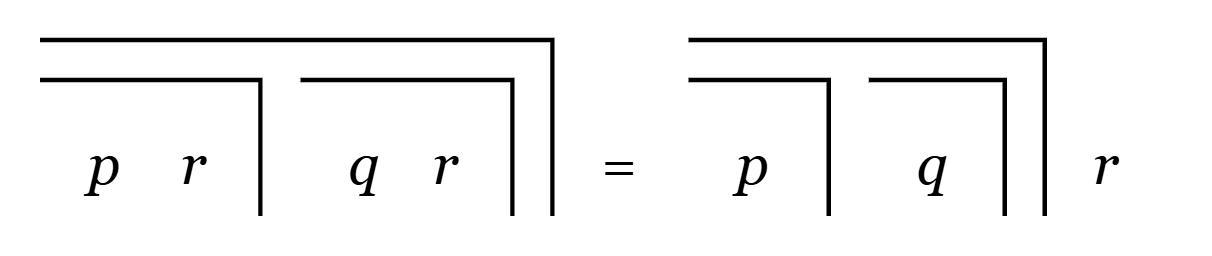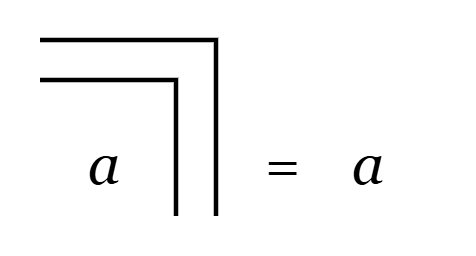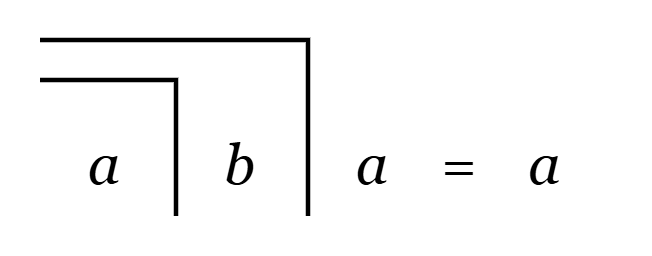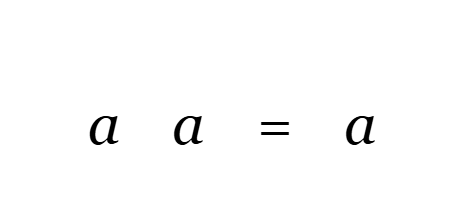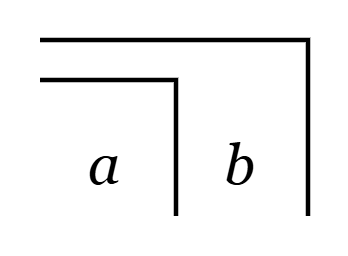Perfect Continence

Recalling the Calculus of Indications

We learn about numbers in school. Nobody tells us what numbers are, except that they represent quantity or position. Instead, we are asked to memorize symbols and combinations of symbols for each number.

There are some strange symbols like zero. We are told it stands for nothing. That's hard to believe. It doesn't look like nothing. It looks like something, and it does things. When put after a different number, a zero magically makes it 10 times bigger. In fact, we can only know what 10 stands for if we memorize that trick.

Then we learn to perform operations with numbers. That, they tell us, is called “arithmetic.”

Later, when a number is not known, that is “algebra.”

We get this layer of magic “for free,” and then all mathematics and science are built on top of it. What it stands on is never questioned.

Almost never.

George Spencer-Brown questioned it in 1969 in his book Laws of Form (LoF). He started earlier, with no assumptions, and went further, in the forbidden territory of self-reference.

He started from nothing. If there is anything different from nothing, that difference can be made by somebody able to make a distinction. Once a distinction is made and indicated, nothing more is required. Distinction is the only constant. Relations of constants are all it takes to make an arithmetic but here it’s even simpler because the constant is also the only relation.

And that relation is containment.

This is the second post in the containment series. You may want to check the previous first, but you don't have to. You can start wherever you want.

Once somebody makes a distinction, that is also the only unique operation. All the rest is repeating: re-calling, re-crossing, re-entering.

The first distinction creates space and invites crossing. The space is a primitive one, without any distance. You can go only from one state to another.

If we indicate a distinction and look at it as both the only constant and the only operation, that's all it takes to have an arithmetic. No numbers, memorization of symbols, magic tricks and taking so many arbitrary things as given.

And, just think about it. Is there a more basic cognitive operation than making a distinction?

Distinction is perfect continence

In the Western tradition, we have the idea of true and false values to judge a proposition. It takes for granted what a proposition is, that it can be understood, evaluated, that there are only two possibilities, true and false, and that they can be distinguished. That's from Aristotle on and didn't change much to this day.

When George Boole created an algebra on this basis, he did not consider the possibility of more than two values, nor what it means for something to have value, before asking what those values might be. To ask what it means for something to have value would already require asking: value for whom? That was not a common question in his time (and it is still rarely asked today). In any case, he created a beautiful, non-numeric algebra. This algebra, however, contained no arithmetic.

George Spencer-Brown attempted to supply the missing arithmetic. He did so without assumptions, grounding it in the most primitive cognitive act: making a distinction. A distinction can only be made by someone, and if what is distinguished is of value, it can be indicated. Out of this, the arithmetic of Laws of Form (LoF) was born. From there, it generated its own algebra. The algebra of Boole, and others, appear only as special cases derivable from it.

The only things that LoF accepts as given are the ideas of distinction and indication. Then, to introduce the laws of form, it needs just one definition:

Distinction is perfect continence.

Making a distinction means drawing a boundary. Like making a circle on a plane, that boundary clearly separates two distinct spaces. In the case of a circle (or a rectangle), we call them inside and outside. One of the meanings of “perfect continence” is that there is no ambiguity when it comes to indication. There cannot be a point on the boundary. It will always be either inside or outside.

The original notation for distinction is what Spencer-Brows calls a mark or a cross, and it looks like that:

In many places, even in the Wikipedia article, it is called a symbol. It's not. Symbols don't illustrate their meaning. The mark does. You can see it as a half-box:

It shows inside and outside, the boundary, and — now with some knowledge about its intent — an invitation to cross that boundary. This is an important and not-so-obvious difference. I’ll be coming back to it a couple of times in what follows.

The distinction is both an operator and an operand, and the only relation in the mathematics of forms: containment.

The distinction is an operator by inviting to cross from one state to the other, and is an operand by being an indication of a state. This action/value duality has important mathematical and philosophical implications.

Distinction is the act of creating something from nothing. From void.

Void is often imagined as empty space. But that is already something: space. If there is space, that's not nothing. Space is what the first distinction creates. Not a space with the notion of distance; more primitive than that. A space where the only “distance” that can be traveled is from a marked space to an unmarked space and back.

Re-calling (condensation)

Axioms are premises that are given. They are not questioned. They cannot be experienced or demonstrated.

The axioms of the calculus of indications, in contrast, are open to examination. These axioms are the two laws of form that give the book its name.

The first axiom is the law of calling.

The value of a call made again is the value of the call.

In other words, to recall is to call.

In the original notation, the expression of that axiom looks like this:¹

This is the form of condensation.

Our keyboards don't have this sign. Even if they did, nesting would be challenging. An alternative way to write such expression is by using parentheses (or any other brackets). The law of calling, then, would look like this:

\(( )( )=( ) \)

This is convenient but comes at the cost of imposing sequence. That’s a limitation. William Bricken explains:

Symbolic notation imposes sequence, suppressing the inherent parallelism of containment structures. Given sufficient processors we can access any number of containers all at the same time, but we cannot read a page of words all at the same time.²

Back to the axiom: to recall is to call. Two (or more marks) next to one another (not nested) condense into one.

How can you imagine the logic of that?

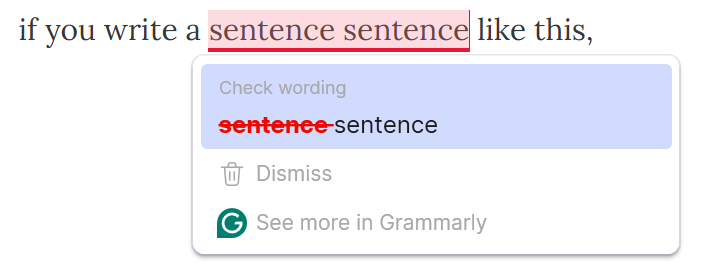
One simple way to see it, is to switch on your writing assistant like Grammarly, QuillBot, Scribendi or whatever you are using. Then,

The two calls “sentence” have the same value, so you are invited to condense them into one.

That is not the case with “he said that that book was the best,” because each that makes a different indication. The first one indicates the statement and the second indicates the book the statement is about. Or “this is the second post in the series; check out the first first,” where the first first indicates the order of writing and the second first, the order of reading.

Another way to imagine it is highlighting. If you highlight some text and if you then highlight it again, you'll have the same number of highlights, one.

This axiom is also the first initial of the primary arithmetic. Since it can be used in both directions, it can be written like this:

\(( ) ( ) ⇌ ( )\)

Going from left to right is to condense, and from right to left is to confirm.

The sign ⇀ represents a step and means “is changed to.”

Re-crossing (cancellation)

The second axiom is the law of crossing. It states the following

The value of a crossing made again is not the value of the crossing.

In other words, to re-cross is not to cross.

In the original notation, it looks like this:

This is the form of cancellation. Two tested crosses are equal to none.

Using parentheses, it can be written like this:

\((()) =\)

The expression is not unfinished. Simply the right side equals to nothing and that is why there is nothing written on the right side.

One way to imagine it is by being outside of a plot, entirely surrounded by a fence. Only two states are of value: you being inside or outside. If you jump over the fence, your state is changed. You are inside. That's the first crossing. If you cross the fence again, no matter where, you'll get outside. You were outside before the crossing and after making two crossings. So, making two crossings, when it comes to distinguishing only being outside versus being inside, is the same as having made no crossing.

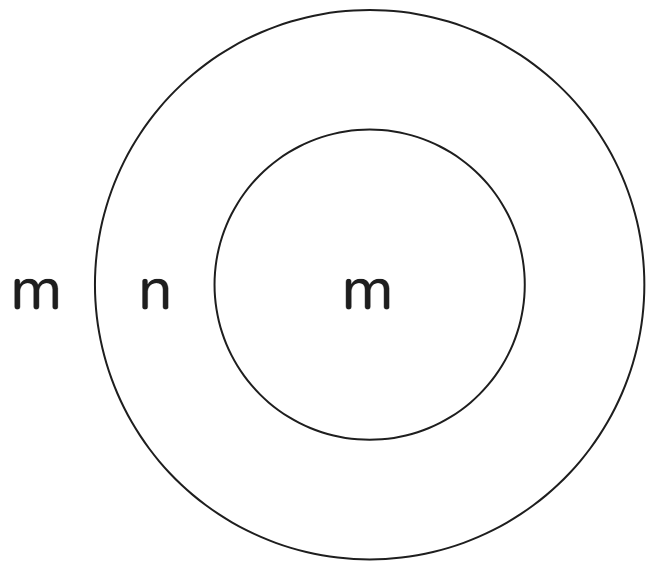
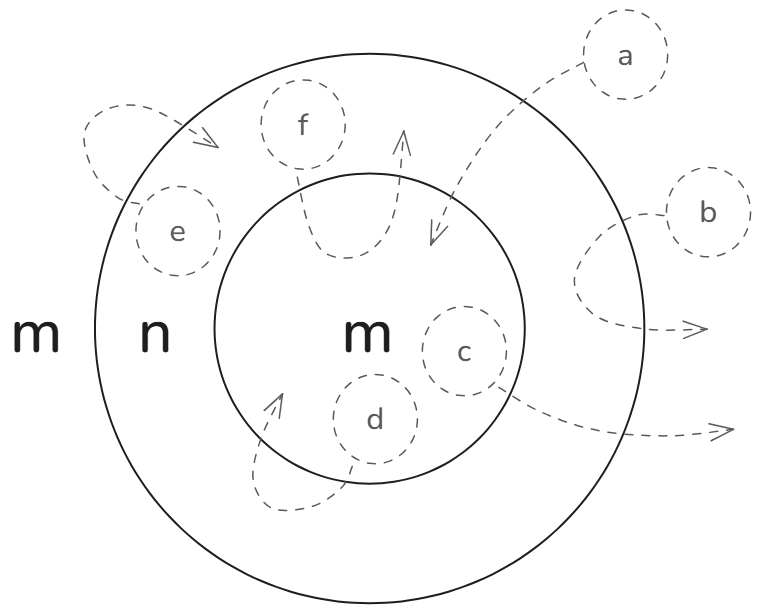
Here's another way to see this. Let's have one circle drawn inside another.

Let's indicate the outside of the outer circle with m for “marked.”

If we cross it, we'll go to the unmarked space. Let's indicate that with n. And if we then cross the inner circle, that will be again a change of state and the inner area will be marked.

There are four possible trajectories for making two crossings starting for a marked space, indicated with a, b, c, and d. Trajectory a is for going from outside the outer circle and crossing the inner. Trajectory b is when the second crossing is of the same outer circle.

Then from the inner marked space, c, is for crossing the two circles from the inside of the smaller one, and d is for crossing once and a second time back.

For a point in the unmarked state, there are two possibilities: crossing outside and back (e), and crossing inside and back (f).

In all six cases, double crossing is the same as no crossing; the initial state is unchanged.

The second axiom is also the second initial of the primary arithmetic. Since it can be used in both directions, it can be expressed like this:

\((( )) ⇌ \)

Going from left to right is to cancel, and going from right to left is to compensate.

With these two axioms, every arrangement has a unique simplification, which is either the marked or unmarked state. A form like this, for example

can be simplified. The order of simplification doesn’t matter. Each time, either the law of calling or the law of crossing is applied until it reaches either the marked state or the unmarked state, where it can’t be simplified any further.

The form above resolves into the unmarked state.

Knowing now the two axioms, it will be easier to show the benefits of using notation that (1) illustrates its meaning, and (2) doesn’t impose sequence.

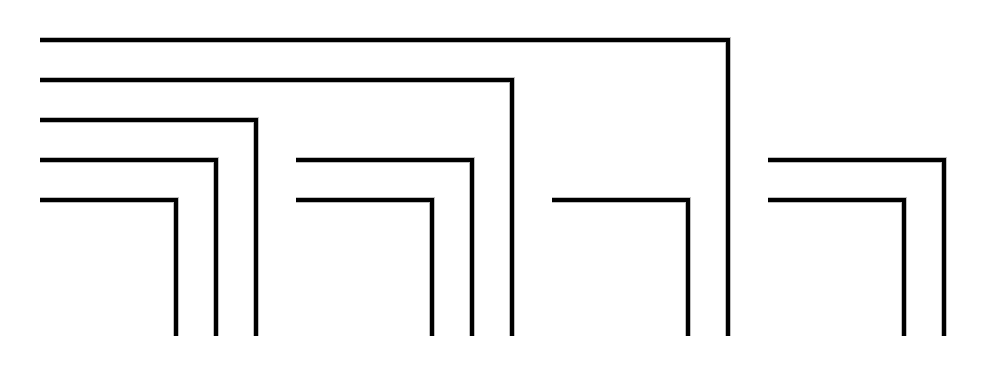
Consider the following arrangement of three numeric constants:

It is meaningless as a whole. You need a different arrangement and additional symbols to calculate it. In contrast, this arrangement

is unambiguous. By the law of calling, the three rectangles can be condensed into one and evaluated as the marked state. Then it may generate endless equivalent forms, for example, this one:

Primary Algebra

In Chapter 3, we are told to:

Call calculation a procedure by which, as a consequence of
steps, a form is changed for another, and call a system of
constructions and conventions which allows calculation a
calculus.

That may be taken as two definitions, of calculation and calculus. Being given in the form of instruction, it reminds us that every definition is just a convention.

We are then told to call the calculus of primary arithmetic, primary algebra.

The identities of primary algebra are indexed with J for the initials, C for consequence. Here are the two initials, J1 and J2, and some of the consequences (only those that we’ll need later).

J1 (Position)

The step from left to right is the action take out, and the one from right to left is put in.

J2 (Transposition)

The step from left to right is the action collect, applied on r, and the one from right to left is distribute.

The first consequence that is reached by applying the transformation steps is called reflection:

C1 (Reflection)

Here is one more:

C4 (Occultation)

The step from left to right is the action conceal, and the one from right to left is to reveal.

And here is the last one we’ll need:

C5 (Iteration)

Self-reference (re-entry)

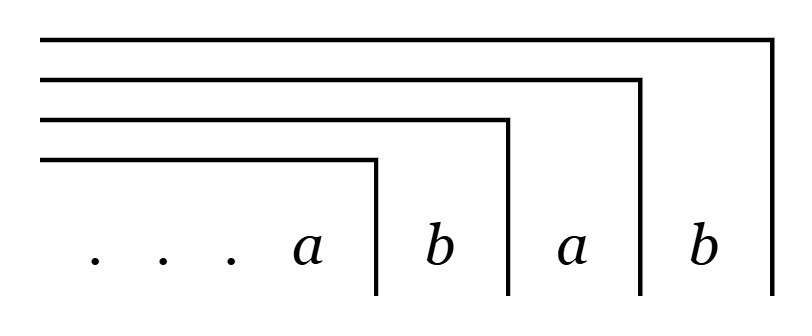
Chapter 11 goes into equations of the second degree. It starts with the expression

and after transformational steps applying the identities of the primary algebra,³ it is turned into an infinite expression:

By just replacing (a(b)) with identical forms, it can be converted into an endless ((((…a)b)a)b). But that also means that (a(b)) in any even depth of ((((…a)b)a)b) is identical with the whole ((((…a)b)a)b). It is in this way that ((((…a)b)a)b) re-enters “its own inner space at any even depth.”

Now it gets really interesting.

If the whole expression is represented by f, it takes this form:

Or more generally:

If f is marked, it is unmarked, and if f is unmarked, it is marked.

Here, f, similar to the mark, has a dual nature. Walter Tydecks explains:

By f is meant both the function (the algorithm, the process) with which a limit value is approximated in infinitely many steps, and the result of the process (this limit value itself). Spencer-Brown consistently holds out his idea of introducing symbols which, in multiple meanings, can be both an operation and the result of that operation.⁴

The expression

has no solution in the primary arithmetic. If the cross on the right side was nested in another, f can be either marked or it can be unmarked, but with a single cross, it indicates both marked and unmarked states.

It has a solution, but not in space, in time. It creates time. In the same way, drawing a distinction creates space, the reentry creates time. But just as the space created by the mark is primitive, without any measure (the only “distance” that can be crossed being from marked to unmarked space and back), this primitive time is time without duration, just oscillation between marked and unmarked state.

The reentry can be illustrated by extending the mark encompassing the re-entrant part of the expression. This way, with minimum visual complication, it shows reentry, what reenters and where.

Here we once again see the benefits of an iconic notation over a symbolic one. We have to know the convention that the symbols a and b represent variables, and stand for any number of crosses. In contrast, the mark and the re-entrant mark (in LoF both referred to as markers), illustrate their meaning.

Yet, as the simple mark, the reentrant one is so minimalistic, it’s worth clarifying what it indicates and how.

Remember, the mark (cross) illustrates a containment. The starting expression ((a)b) can be represented by a container containing b and containing another container, which contains only a.

The snake-like extension of the outer cross illustrates reentry of the whole expression and shows where in the space it indicates, it reenters. In the container diagram, it can be shown like this:

resulting in

That’s how this form

illustrates its meaning. In the words of Louis H. Kauffman, it’s an “infinite in finite guise.”

Reentries in space represent self-referential expressions like “this statement is false.” Any attempt to solve it produces a contradiction. It’s not meaningless, so it must be either true or false. If it is true, then it must be false, as it states. But if it is false, then saying that it is false makes it true.

Paradoxes are well known from Antiquity but rarely liked. It was formative for Western logic to try to avoid them, to treat them as errors. The Aristotelian laws of identity, excluded middle and non-contradiction are still regarded as the three laws of thought. Bertrand Russel, who discovered an important paradox in set theory now bearing his name, did his best in his theory of types to outlaw paradoxes.

Spencer-Brown, who was a student of Russel, made the following comment on this:

When you do this peculiar thing of making something self-referential that is making the answer go back into the expression out of which the answer comes, you now automatically produce this set of possibilities which are well-known in numerical mathematics and of which everyone's been terrified of looking at in Boolean mathematics. And Russell/Whitehead were so frightened of these, that they just had a rule with no justification whatsoever that we just don't allow it, we don't even allow people to think about this.⁵

And no reasoning is given why self-reference doesn’t exist, and on the basis of what it should be excluded. Spencer-Brown again:

And this is so awful, so terrifying, that they said, "Right. We will produce a rule. We call it the Theory of Types to give it a grand name." The Theory of Types says — it is as much unlike what it says as possible, so that when someone says, "Well, what is the rule by which you can't have this?" — "It's the Theory of types," so that the people who are learning think that there is a huge theory, you see, and when you understand this theory you will realize why it is that you can't have such a thing.

While Western thought has always been afraid of self-reference, the logicians and philosophers from the East embraced it. By the time Aristotle came up with the laws of identity, excluded middle and non-contradiction, several thousand miles to the east, in northern India, the Catuṣkoṭi system was born.

Catuṣkoṭi means four corners. It is a logical system that accepts that a given proposition can be — if translated into the Western values of true and false — true, false, neither true nor false (e.g. a proposition about the future), both true and false (self-reference).

Most likely, a Catuṣkoṭi practitioner learning about Aristotelian laws would find them contingent and arbitrary.

One of the reasons to keep away from the paradox is that it was always considered, in the West, an impossibility. Ironically, Spencer-Brown discovered the need to include them when he left the department of mathematics at Cambridge and worked to solve practical engineering problems in railways.

One simple way to not only see the possibility but also the practical application of LoF reentry is the classic electrical bell.

When current passes through an electromagnet, it attracts an armature connected to a hammer that strikes the bell. The same armature opens a contact in the circuit, and with no running electricity, the electromagnet loses its pull. The armature springs back, closing the circuit again, so the electromagnet pulls, and the hammer strikes again, opening the circuit. The oscillation goes on as long as the electric bell button is held down.

In reentry terms, when the circuit is closed and current is running, then it is in a marked state, and when it is open, it is in an unmarked state. The bell works due to the oscillation.

Self-reference is more fundamental than what an electrical device illustrates. It made some of the greatest minds of the last century rethink reality, life and society.

Heinz von Foerster, in his paper Objects: tokens of (eigen) behaviours,⁶ challenged the idea that objects are “out there,” independent of our cognition. They are rather stable patterns, constructed by the circular nature of perception and action.

It might be that objects are constructed by life through looping coordinations. But that’s not so easy to see. However, it is easier to see that life itself is characterized by self-reference. Life happens because of operational closure, which produces autonomy, and in the strong case, the living cell, autopoiesis. The cell produces itself, including its boundary, the semipermeable membrane, which makes the production processes possible (without it, the molecules won’t enter into synthetic reactions). This operational closure happens at other levels, such as the immune system, the nervous system, and the organism as a whole.

Seeing that autonomy is a defining characteristic of life, and that it is a matter of self-reference, Varela extended the calculus of indications to include reentry as a separate value. He presented a short proposal in a short paper in 1975⁷ and a more extended version in Principles of Biological Autonomy.⁸

If Velara used LoF to give a mathematical form of the defining feature of living systems, Luhmann used it to create a grand theory of social systems.⁹ It is a monumental, radically constructivist attempt to describe modern society. While LoF is just one tiny book, Luhmann’s Systems theory is described in dozens of books and hundreds of papers.¹⁰ And although Luhmann didn’t use any formulas, he wrote with a similar level of rigour.

Social systems, according to Luhmann, are made up of a self-referential network of communications, which maintains the boundary between system and environment by making a distinction between self-reference and other reference. Different functional subsystems, such as the economy, politics, science, law, religion, art, education, and mass media, are operationally closed, self-producing, and working according to their internal binary code. This code is the distinction between legal/illegal in law, true/untrue in science and beautiful/ugly in art. This binary code reenters the systems when the systems use it to observe it. For example, science observes its use of the code true/untrue using the same code true/untrue.

Organizations are a specific kind of social system, where the communication events that make up the constituting self-referential network are decisions. Decisions are self-referential and paradoxical. Every decision has to communicate its alternatives (if there were no alternatives, it’s not a decision), which enables regret, criticism and blame. At the same time, a decision has to communicate that it is not any of its alternatives, otherwise it’s not a decision.

What is a decision is also a decision. Decisions are created backward by future decisions pointing to a previous one as its premise, making it an actual decision this way.

Decisions also enable a reentry of time into time: a decision event making a difference between not-decided/decided happens in a certain moment. Every moment already makes a difference between past and future, hence the reentry. This part deserves to be quoted in full.

Every decision presupposes world time, which continuously moves the distinction between past and future into a different, a new present. Only rough simplification allows us to understand this as a movement or process. In fact, every present is burdened with the problems of redescribing its past and reprojecting its future. However, time allows little time to do so. Reflections of this sort can therefore only be highly selective and undertaken only for special reasons.

This problem is, as it were, copied in the decision. It establishes a past that is relevant for it, and therefore requires a memory that helps it to understand problems, alternatives, and resources as aspects of its present. Moreover, a decision can occur only if those involved understand that it makes a difference. If the decision is made, the world will look different from what it would if it were not made. The projection of a difference is therefore an integral part of decision-making. A decision constructs a different context of past and future than that which otherwise exists in world time. But this happens in the world, and hence in world time, for example, at a datable point in time. What occurs is a “reentry” of time into time, or, more precisely, of the distinction between past and future into the distinction between past and future.¹¹

Coda

Laws of Form inspired people from different arts: mathematics, biology, psychology, cybernetics, philosophy, music, cognitive, computer and social sciences. Naturally, it also attracted criticism. Some claim that it is just another notation for Boolean algebra, others that it is simply isomorphic to symbolic logic. There are some good attempts to show why this is not the case. If you are interested to follow these arguments, I invite you to study Distinction is Sufficient (link in the footnotes).

Whatever the case, George Spencer-Brown showed that with only one relation, containment, a whole calculus can be created. Unlike other systems, it takes into account the observer and elegantly deals with self-reference, providing a new way to understand space and time and to think about thinking.

1. All expressions in the original notation of Laws of Form, are created using FORM tricorder.

2. Source: Distinction is sufficient.

3. Here are the transformations:

Start with

Applying C5, we double it into

And then we replace the first b with ((b)), in other words, we reflect it, courtesy of C1, and get

J2 allows us to distribute ((a)b) to the second depth of nesting on the left, which means that ((a)b) will go next to the first a and next to (b), resulting in

Note that the ordering is simply following the rule that the depth of nesting increases from right to left, so in the form above, you see ((a)b), which is the r from J2, is positioned on the left side of a and (b) respectively.

In the book, the next form is supposed to be reached just by applying C4

This can be reached, but only if applying other intermediate transformations, before C4. In this video, Leon Conrad shows how it can be reached via C1, J2, C5, C1, C4 steps.

Then by replacing ((b)) with b as per C1, we get

These transformations can be applied to the deepest ((a)b) infinitely, and that’s how we get to

4. Tydecks, W. (n.d.). A commentary on Laws of Form from Spencer-Brown. Retrieved September 24, 2025, from http://www.tydecks.info/online/themen_e_spencer_brown_logik.html

5. Source: AUM Conference 1973 transcripts

6. This paper was published in 1976, as a tribute to Jean Piaget, who turned 80 that year. A few years previously, Heinz von Foerster, wrote a glowing review of Laws of Form in the Whole Earth Catalog. Although he didn’t cite LoF in the 1976 paper, it most certainly influenced his work, for which self-reference was of central importance. Objects: tokens of (eigen) behaviours continues to be influential today. A whole 2017 issue of Constructivist Foundations, was devoted to it, with contributions from eminent mathematicians, cognitive and complexity scientists and philosophers.

7. FRANCISCO, J., & VARELA, G. (1975). A Calculus for Self-Reference. International Journal of General Systems, 2(1), 5–24. https://doi.org/10.1080/03081077508960828

8. That book for out of print for a long time, but luckily a new edition was recently published, edited and annotated by Ezequiel Di Paolo and Evan Thompson.

9. Luhmann laid the foundations of his Systems Theory in the 60s and 70s, but it took it shape of 80s on. The theory was first described in Social Systems (1984) and had it's full blown form in his magnum opus, which was also his last work, the two volume Theory of Society (1997). Between them he described different functional sub-system as those of Law, Art, and Religion, as well as specific social systems such us organizations, described already in Organization and Decision, published in 1978.

10. Luhmann was a prolific writer. The counting has not finished, but the preliminary catalogue of Luhmann’s archive, published in 2022, listed 1464 works, of which 552 of these are unpublished. The major single-authored published books are over 50.

11. Luhmann, N., Baecker, D., & Barrett, R. (2018). Organization and decision. Cambridge University Press. https://doi.org/10.1017/9781108560672 (Original work published 1978)